Note: This didn’t handle 3 digit MNCs, an updated version is available here and in the code sample below.
The PLMN Identifier is used to identify the radio networks in use, it’s made up of the MCC – Mobile Country Code and MNC – Mobile Network Code.
But sadly it’s not as simple as just concatenating MCC and MNC like in the IMSI, there’s a bit more to it.
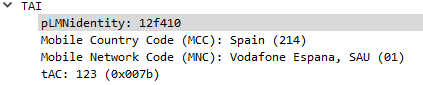
In the example above the Tracking Area Identity includes the PLMN Identity, and Wireshark has been kind enough to split it out into MCC and MNC, but how does it get that from the value 12f410?
This one took me longer to work out than I’d like to admit, and saw me looking through the GSM spec, but here goes:
PLMN Contents: Mobile Country Code (MCC) followed by the Mobile Network Code (MNC).
TS GSM 04.08 [14].
Coding: according to TS GSM 04.08 [14].
If storage for fewer than the maximum possible number n is required, the excess bytes shall be set to ‘FF’. For instance, using 246 for the MCC and 81 for the MNC and if this is the first and only PLMN, the contents reads as follows: Bytes 1-3: ’42’ ‘F6′ ’18’ Bytes 4-6: ‘FF’ ‘FF’ ‘FF’ etc.
Making sense to you now? Me neither.
Here’s the Python code I wrote to encode MCC and MNCs to PLMN Identifiers and to decode PLMN into MCC and MNC, and then we’ll talk about what’s happening:
def Reverse(str):
stringlength=len(str)
slicedString=str[stringlength::-1]
return (slicedString)
def DecodePLMN(plmn):
print("Decoding PLMN: " + str(plmn))
if "f" in plmn:
mcc = Reverse(plmn[0:2]) + Reverse(plmn[2:4]).replace('f', '')
print("Decoded MCC: " + str(mcc))
mnc = Reverse(plmn[4:6])
else:
mcc = Reverse(plmn[0:2]) + Reverse(plmn[2:4][1])
print("Decoded MCC: " + str(mcc))
mnc = Reverse(plmn[4:6]) + str(Reverse(plmn[2:4][0]))
print("Decoded MNC: " + str(mnc))
return mcc, mnc
def EncodePLMN(mcc, mnc):
plmn = list('XXXXXX')
if len(mnc) == 2:
plmn[0] = Reverse(mcc)[1]
plmn[1] = Reverse(mcc)[2]
plmn[2] = "f"
plmn[3] = Reverse(mcc)[0]
plmn[4] = Reverse(mnc)[0]
plmn[5] = Reverse(mnc)[1]
plmn_list = plmn
plmn = ''
else:
plmn[0] = Reverse(mcc)[1]
plmn[1] = Reverse(mcc)[2]
plmn[2] = Reverse(mnc)[0]
plmn[3] = Reverse(mcc)[0]
plmn[4] = Reverse(mnc)[1]
plmn[5] = Reverse(mnc)[2]
plmn_list = plmn
plmn = ''
for bits in plmn_list:
plmn = plmn + bits
print("Encoded PLMN: " + str(plmn))
return plmn
EncodePLMN('505', '93')
EncodePLMN('310', '410')
DecodePLMN("05f539")
DecodePLMN("130014")In the above example I take MCC 505 (Australia) and MCC 93 and generate the PLMN ID 05f539.
The first step in decoding is to take the first two bits (in our case 05 and reverse them – 50, then we take the third and fourth bits (f5) and reverse them too, and strip the letter f, now we have just 5. We join that with what we had earlier and there’s our MCC – 505.
Next we get our MNC, for this we take bytes 5 & 6 (39) and reverse them, and there’s our MNC – 93.
Together we’ve got MCC 505 and MNC 93.
https://www.cisco.com/c/en/us/td/docs/wireless/asr_5000/21-11_6-5/GTPP-Reference/21-11-GTPP-Reference/21-11-GTPP-Reference_chapter_01001.html#reference_4aed2774-e602-4d96-b921-7d3a0b0ba00f
Look at: “The following subclauses specify the coding of the different identities. For each identity, if an Administration decides to include only two digits in the MNC, then bits 5 to 8 of octet 7 are coded as “1111”. ”
In some coutries (like US) MNC is 3 digits not 2 and there is no f in PLMN_ID
It is like that to help distinguish 2 and 3 digit long MNCs AFAIK
>> why not just encode 50593? What is gained by encoding it as 05f539?
Not sure how relevant this question is almost 2 years later, but I’ll chime in anyway: it is to minimize the value weight in bytes.
In this encoded way, it takes 3 bytes to pass PLMN value (regardless if 5 or 6 digits PLMNs).
Sending it plain (in UTF-8, for example) would require 5 bytes – 0x35:30:35:39:33 (50593 in UTF-8/ASCII) and 6 bytes for 6-digits PLMN.
2 or 3 bytes sound negligible, but when you scale things to telecoms levels of signaling messages being sent back and forth within and between networks (roaming), that difference becomes noticeable – less traffic to send.
As Aleksei says here, the PLMNIdentifier will be encoded into 3 bytes, and such format is called BCD (https://en.wikipedia.org/wiki/Binary-coded_decimal). In telecommunications, most numbers are encoded in this way, like the phone number, IMEI, IMSI, etc. If the number of digits is odd, normally an F will be appended.