Chances are if you’re reading this, you’re trying to work out what Telephony Binary-Coded Decimal encoding is. I got you.
Again I found myself staring at encoding trying to guess how it worked, reading references that looped into other references, in this case I was encoding MSISDN AVPs in Diameter.
How to Encode a number using Telephony Binary-Coded Decimal encoding?
First, Group all the numbers into pairs, and reverse each pair.
So a phone number of 123456, becomes:
214365
Because 1 & 2 are swapped to become 21, 3 & 4 are swapped to become 34, 5 & 6 become 65, that’s how we get that result.
TBCD Encoding of numbers with an Odd Length?
If we’ve got an odd-number of digits, we add an F on the end and still flip the digits,
For example 789, we add the F to the end to pad it to an even length, and then flip each pair of digits, so it becomes:
87F9
That’s the abbreviated version of it. If you’re only encoding numbers that’s all you’ll need to know.
Detail Overload
Because the numbers 0-9 can be encoded using only 4 bits, the need for a whole 8 bit byte to store this information is considered excessive.
For example 1 represented as a binary 8-bit byte would be 00000001, while 9 would be 00001001, so even with our largest number, the first 4 bits would always going to be 0000 – we’d only use half the available space.
So TBCD encoding stores two numbers in each Byte (1 number in the first 4 bits, one number in the second 4 bits).
To go back to our previous example, 1 represented as a binary 4-bit word would be 0001, while 9 would be 1001. These are then swapped and concatenated, so the number 19 becomes 1001 0001 which is hex 0x91.
Let’s do another example, 82, so 8 represented as a 4-bit word is 1000 and 2 as a 4-bit word is 0010. We then swap the order and concatenate to get 00101000 which is hex 0x28 from our inputted 82.
Final example will be a 3 digit number, 123. As we saw earlier we’ll add an F to the end for padding, and then encode as we would any other number,
F is encoded as 1111.
1 becomes 0001, 2 becomes 0010, 3 becomes 0011 and F becomes 1111. Reverse each pair and concatenate 00100001 11110011 or hex 0x21 0xF3.
Special Symbols (#, * and friends)
Because TBCD Encoding was designed for use in Telephony networks, the # and * symbols are also present, as they are on a telephone keypad.
Astute readers may have noticed that so far we’ve covered 0-9 and F, which still doesn’t use all the available space in the 4 bit area.
The extended DTMF keys of A, B & C are also valid in TBCD (The D key was sacrificed to get the F in).
| Symbol | 4 Bit Word | |
| * | 1 0 1 0 | |
| # | 1 0 1 1 | |
| a | 1 1 0 0 | |
| b | 1 1 0 1 | |
| c | 1 1 1 0 |
So let’s run through some more examples,
*21 is an odd length, so we’ll slap an F on the end (*21F), and then encoded each pair of values into bytes, so * becomes 1010, 2 becomes 0010. Swap them and concatenate for our first byte of 00101010 (Hex 0x2A). F our second byte 1F, 1 becomes 0001 and F becomes 1111. Swap and concatenate to get 11110001 (Hex 0xF1). So *21 becomes 0x2A 0xF1.
And as promised, some Python code from PyHSS that does it for you:
def TBCD_special_chars(self, input):
if input == "*":
return "1010"
elif input == "#":
return "1011"
elif input == "a":
return "1100"
elif input == "b":
return "1101"
elif input == "c":
return "1100"
else:
print("input " + str(input) + " is not a special char, converting to bin ")
return ("{:04b}".format(int(input)))
def TBCD_encode(self, input):
print("TBCD_encode input value is " + str(input))
offset = 0
output = ''
matches = ['*', '#', 'a', 'b', 'c']
while offset < len(input):
if len(input[offset:offset+2]) == 2:
bit = input[offset:offset+2] #Get two digits at a time
bit = bit[::-1] #Reverse them
#Check if *, #, a, b or c
if any(x in bit for x in matches):
new_bit = ''
new_bit = new_bit + str(TBCD_special_chars(bit[0]))
new_bit = new_bit + str(TBCD_special_chars(bit[1]))
bit = str(int(new_bit, 2))
output = output + bit
offset = offset + 2
else:
bit = "f" + str(input[offset:offset+2])
output = output + bit
print("TBCD_encode output value is " + str(output))
return output
def TBCD_decode(self, input):
print("TBCD_decode Input value is " + str(input))
offset = 0
output = ''
while offset < len(input):
if "f" not in input[offset:offset+2]:
bit = input[offset:offset+2] #Get two digits at a time
bit = bit[::-1] #Reverse them
output = output + bit
offset = offset + 2
else: #If f in bit strip it
bit = input[offset:offset+2]
output = output + bit[1]
print("TBCD_decode output value is " + str(output))
return output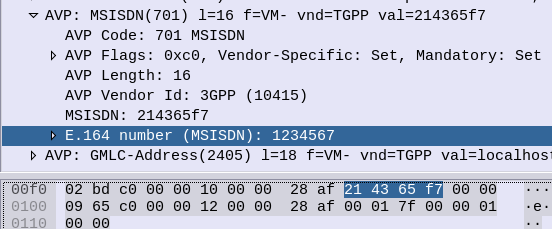
Hi Nick!
Thanks a lot for sharing such invaluable article. I came across your blog exactly while trying to properly encode/decode data to use it for MSISDN and STN-SR AVPs.
Great blog btw!
Cheers!
Forgot to mention there is a typo in PyHSS current code. Instead converting “c” input to “1110” as per table you shared, it is converting to the same value (“1100”) attached to “a” input. Once again, thanks for your article!
Hi Nick,
But there are some problem with the python code…
When the input is “*21”, the output should be “2af1”, but the code output is “42f1”.
Any way the explain of TBCD Encoding helps a lot.
Thank you!
Thank you for your article. It is very useful.